BUAA-OO-Unit1

字数统计: 2.7k阅读时长: 9 min

 2022/03/24 

写在前面：我很满足！助教夸我类图画的好看耶！

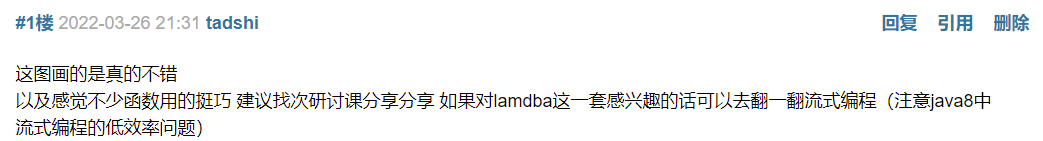
一、程序结构

UML类图与架构设计

第一次作业

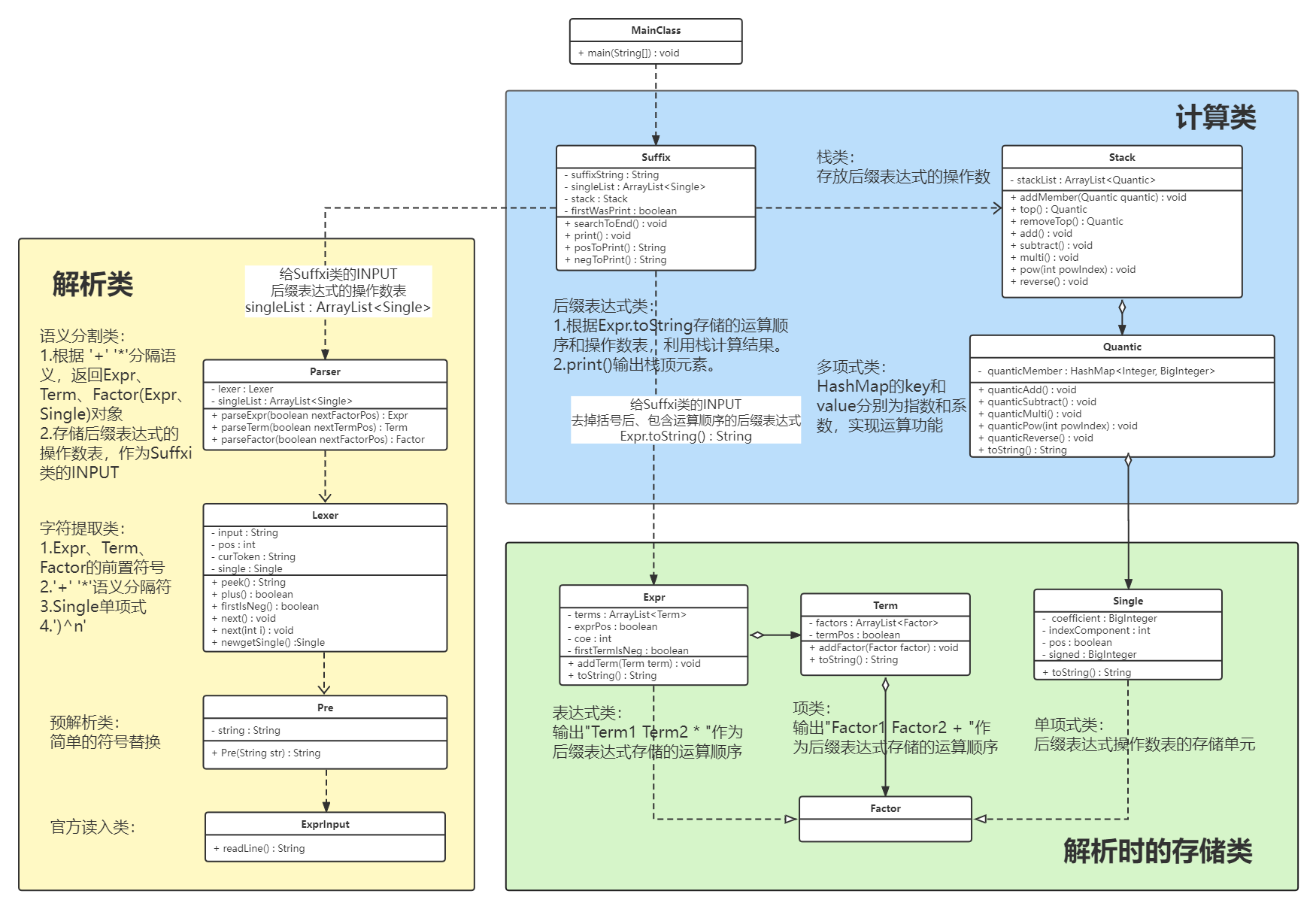
通过Lexer和Parser解析字符串，递归下降生成Expr对象时去除括号
重写Expr.toString()，生成记录运算顺序的后缀表达式SuffixString。格式”X1(操作数) X2(操作数) +(操作符) …”。后缀表达式的操作符包括+、*、^int(表达式因子的幂运算)、!(取反)；
Parser维护了一个后缀表达式操作数表
Suffix类获取包含操作符运算顺序的String和操作数表，用栈进行计算结果得到Quantic对象，对Quantic对象调用print()方法输出。
第二次作业迭代思路：

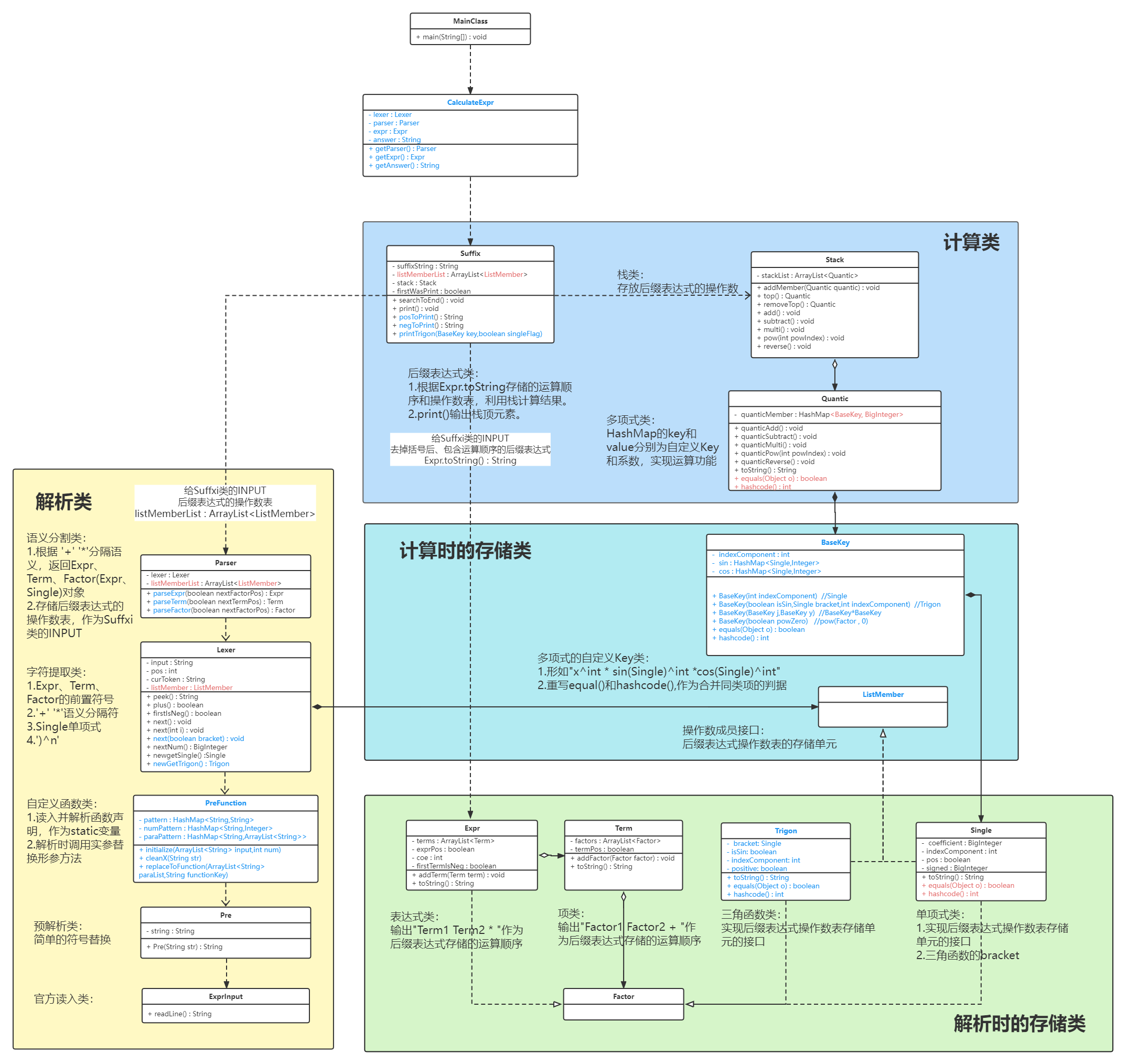
一、引入三角函数后的统一存储形式

多项式的每项基本形式：ax^b -> ax^b(sin容器)(cos容器)
选用hashmap，merge()方法和lambda函数实现合并同类项非常简洁。
- Key为自定义类型BaseKey，重写hashcode()和equal()后便于合并同类项。形式：x^b(sin容器)(cos容器)
- 由于需要维护可变类型BaseKey作为hashmap的key的不可变性，以及value代表的系数为不可变类型BigInteger，没有出现深浅拷贝的Bug

二、sum函数因子的处理

将sum函数作为因子Factor，在递归下降处理表达式中，类似处理表达式因子的模式，进行递归下降处理
具体实现：识别出sum函数的求和表达式，为此表达式新建lexer和parser对象，返回求和后的Expr作为因子。类型为抽象接口Factor

三、自定义函数的处理

新建自定义函数类，类中使用static成员变量存储预先读入的函数形参表和函数表达式
递归下降过程中识别到自定义函数因子时，新建自定义函数类的对象，传入读取到的实参表，返回替换后的Expr作为因子。

第三次作业迭代思路

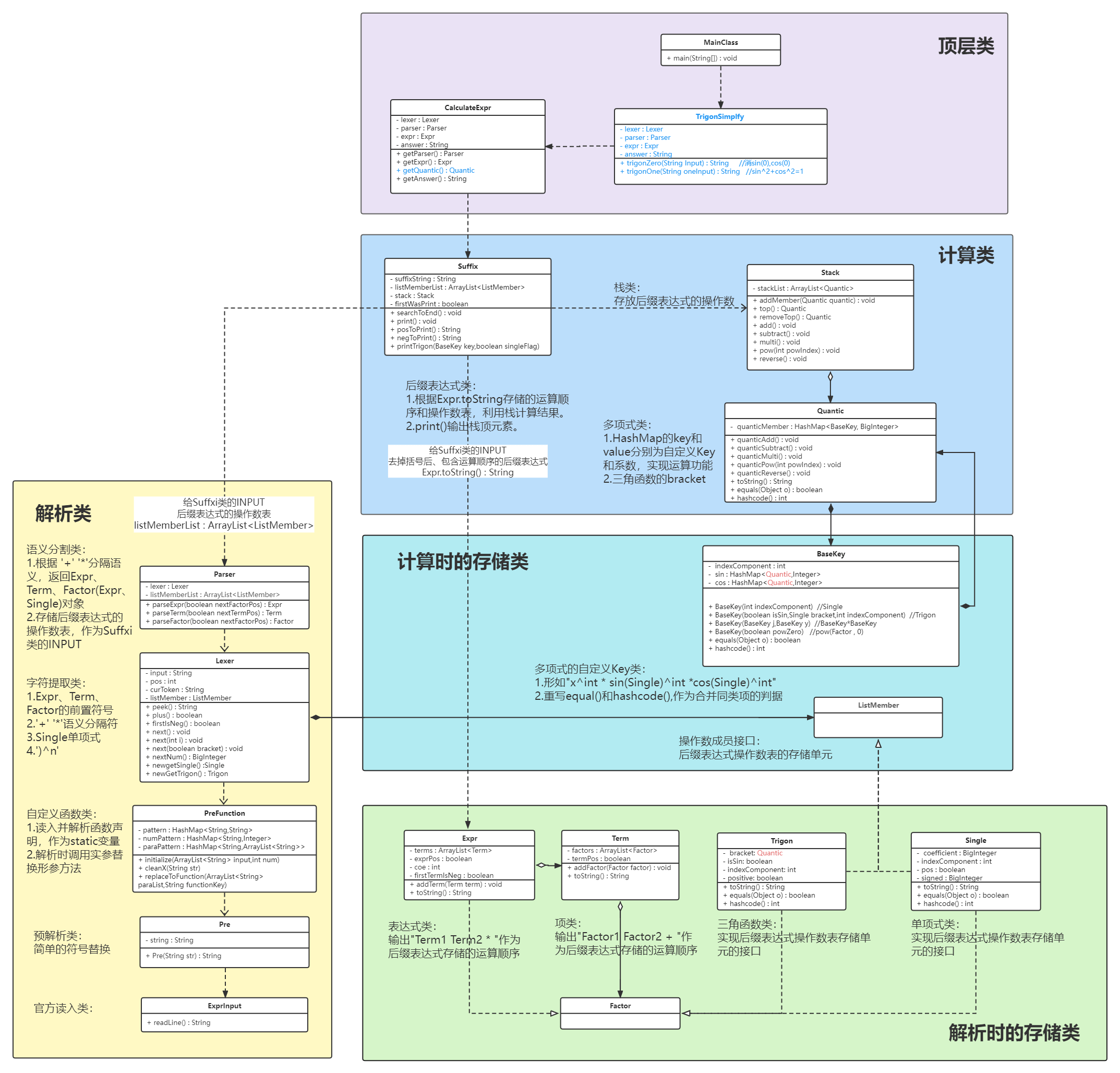
一、嵌套函数：作业二实现

二、三角函数因子为表达式因子

sin(bracket)，bracket类型由Single换为Quantic即可
三、三角函数的化简
sin(0)->(0);cos(0)->(1)，Pre类内字符串替换即可；
sin(bracket)，bracket为常数因子或幂函数因子时去括号。Suffix.print()输出字符串时按有无'+''*'作为常数因子或幂函数因子的判断依据；
诱导公式：括号内负号外提。三角函数符号=f(括号内表达式符号，指数，三角名)，lexer.getTrigon()内处理；
sin(brackt)**2->(1-cos(brackt)**2);CalculateExpr()化简，取最短字符串为结果；
cos(brackt)**2->(1-sin(brackt)**2);CalculateExpr()化简，取最短字符串为结果；

使用的OO度量

度量指标			说明
LCOM	Lack of Cohesion in Methods – Class	方法的内聚缺乏度	值越大，说明类内聚合度越小。
FANIN	Fan-in – Class	类的扇入	表示调用该模块的上级模块的个数，扇入越大，表示该模块的复用性好。
FANOUT	Fan-out – Class	类的扇出	表示该模块直接调用的下级模块的个数，扇出过大表明模块复杂度高，但扇出过小也不好。
OCavg	Average opearation complexity	类的平均操作复杂度
OCmax	Maximum operation complexity	类的最大操作复杂度
WMC	Weighted method complexity	类的加权方法复杂度
CogC	Cognitive complexity	方法的认知复杂度
ev(G)	Essential cyclomatic complexity	方法的基本圈复杂度	衡量程序非结构化程度。
iv(G)	Design complexity	方法的设计复杂度	模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。
v(G)	cyclonmatic complexity	方法的独立路径的条数

类的内聚和相互间的耦合情况

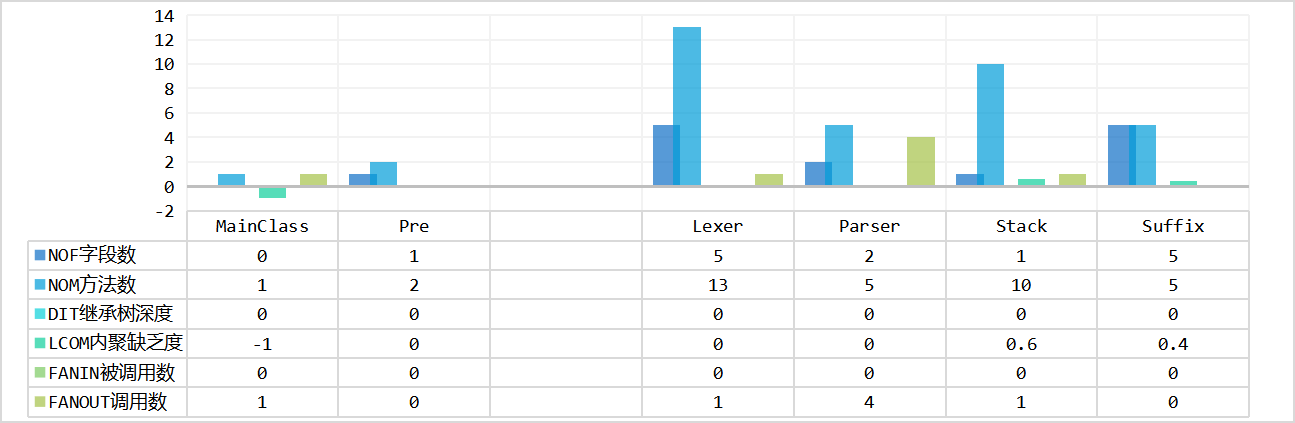
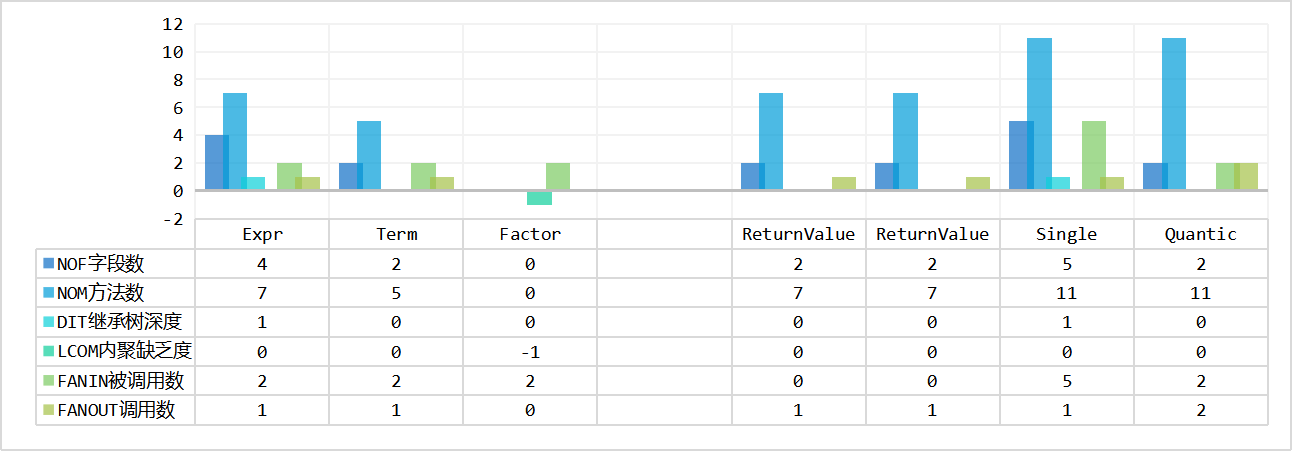
以下为三次作业的类的属性个数、方法个数、LCOM、FANIN、FANOUT。大致依据类的功能分为存储类和执行类分别统计。执行类包括解析、计算、化简输出三部分。

hw1

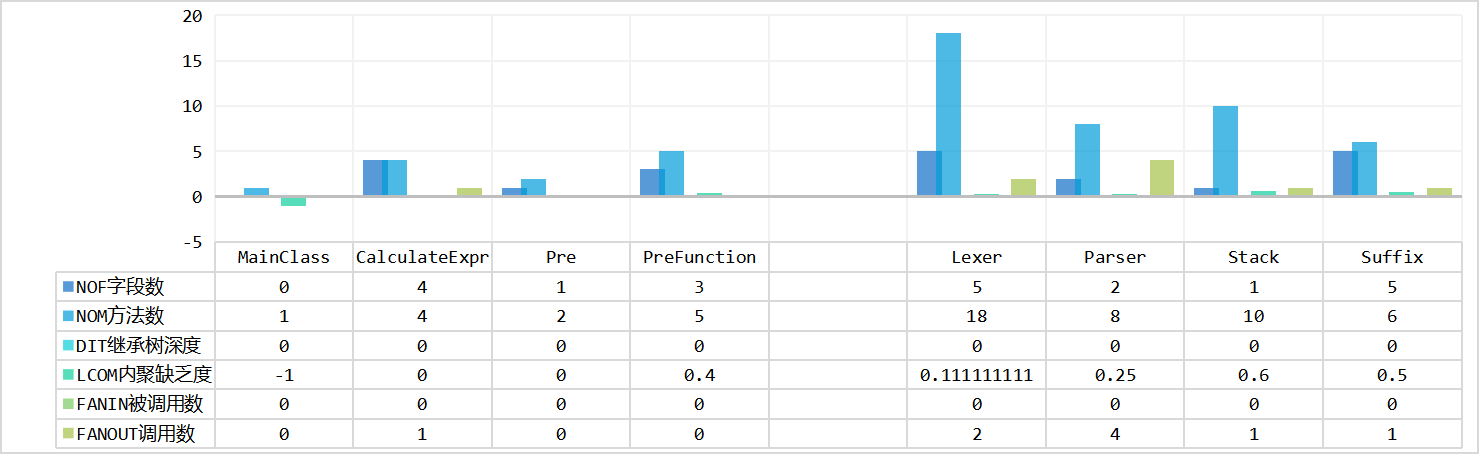
hw2

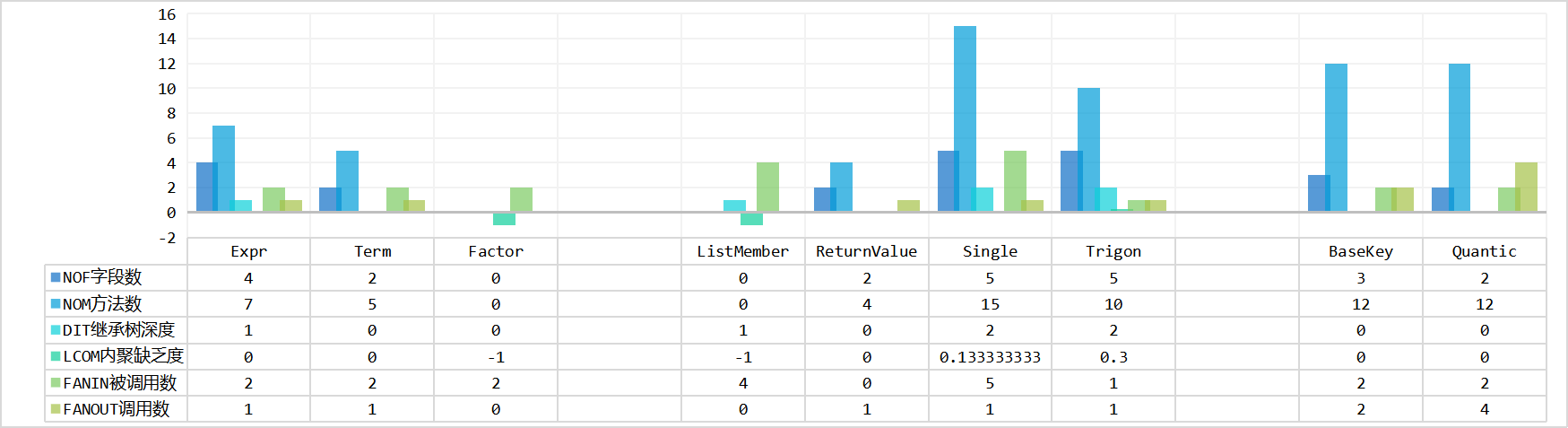
hw3

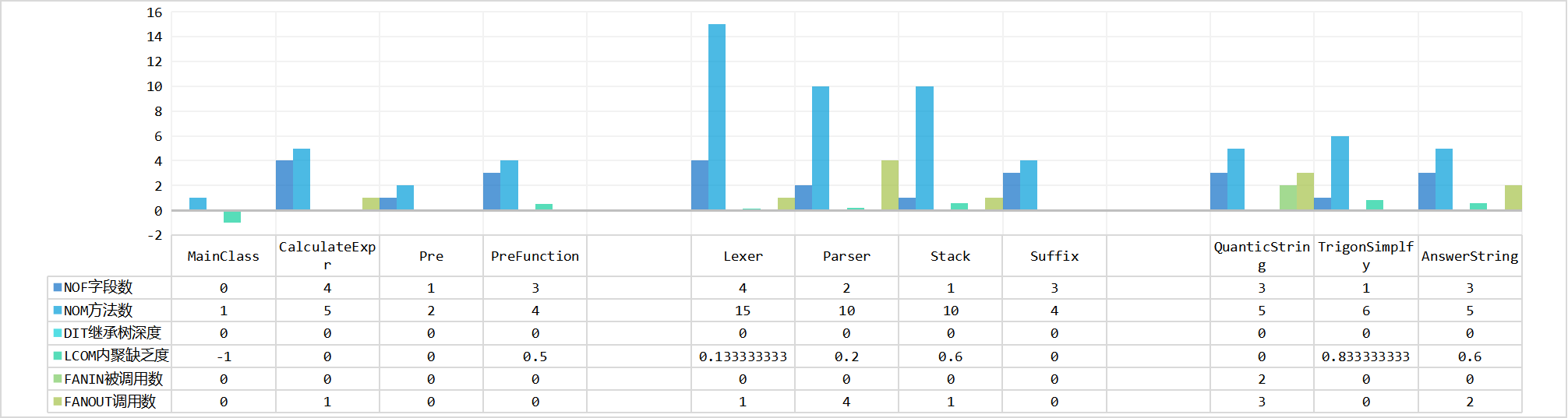
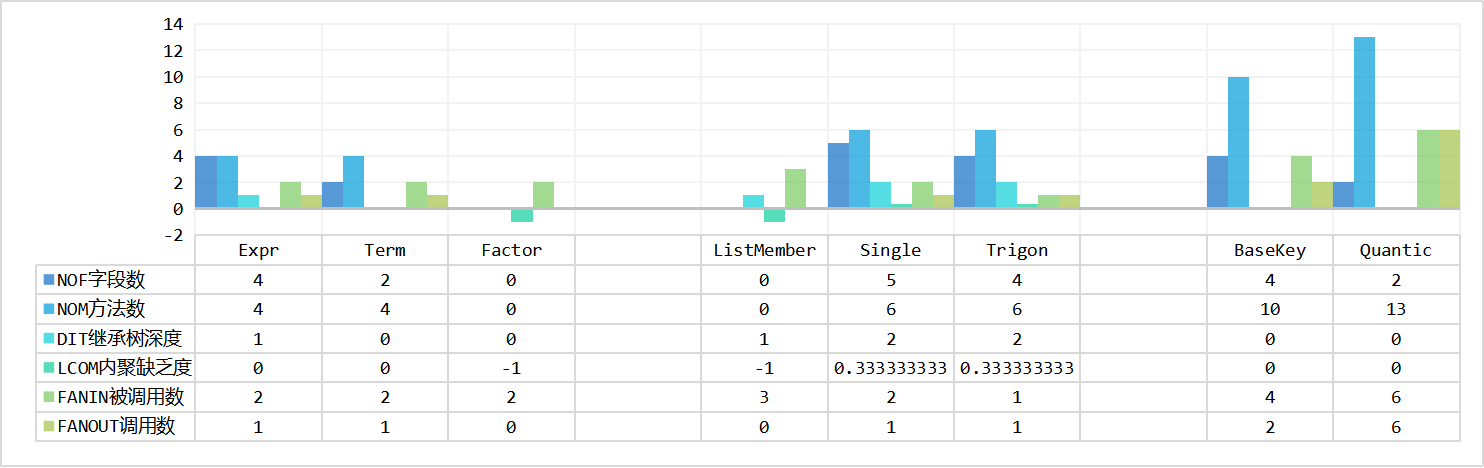
分析：

设计要求高内聚低耦合，即LCOM值要小，FANIN值要大，FANOUT值要合理。

存储类的FANIN明显高于执行类的FANIN

存储类的复用率高：说明存储类型选取的hashmap<BaseKey,BigInteger>较为合适，与同学交流时也发现自己的存储与计算的代码实现较为简洁，hw1-3均使用了Basekey和merge方法，没有过多迭代过程
执行类的复用率低，说明执行类的逻辑仍然存在面向过程性。

LCOM较低，说明方法的高内聚实现较好。

方法的规模与分支复杂度情况

以下为截取hw3的复杂度较高的方法和类，复杂度集中在Lexer、Suffix的符号识别和字符串输出化简两部分。由于分支复杂度较高，这两部分的测试时间和bug也相应较多。

优点

存储类的数据类型选取合适：
- 选用hashmap，merge()方法和lambda函数实现合并同类项非常简洁。
- Key为自定义类型BaseKey，重写hashcode()和equal()后便于合并同类项
- 由于需要维护可变类型BaseKey作为hashmap的key的不可变性，以及value代表的系数为不可变类型BigInteger，没有出现深浅拷贝的Bug

public class Quantic {
    private HashMap<BaseKey, BigInteger> quanticMember;

    public void quanticAdd(Quantic nextTop) {
        nextTop.getQuanticMember().forEach((key, value) ->this.quanticMember.merge(key, value, BigInteger::add));
        //hashmap1合并进hashmap2，类似合并同类项原理
    }

forEach()方法用于对 HashMap 中的每个键值对执行指定的操作。匿名函数 lambda 的表达式作为 forEach()方法的参数传入。
merge()方法用于合并两个hashmap，使用lambda表达式 (oldValue, newValue) -> (oldValue + newValue) 作为重映射函数。
Java 8的方法引用更方便，方法引用由::双冒号操作符标示,使用BigInteger::add作为重映射函数即可
由于hashmap.merge()在插入hashmap2中不存在的key与其对应的value时不会调用重映射函数，故减法不能使用BigInteger::subtract作为映射函数；解决办法为减数先取反，再与被减数调用quanticAdd()即可

乘法将两个BaseKey相乘后的新BaseKey作为merge方法的key参数，系数的乘积作为value参数，重映射函数BigInteger::add

public Quantic quanticMulQuantic(Quantic nextTop) {
      Quantic ans = new Quantic();
      for (BaseKey j : this.quanticMember.keySet()) {
          for (BaseKey y : nextTop.quanticMember.keySet()) {
              BigInteger coeJ = this.quanticMember.get(j);
              BigInteger coeY = nextTop.getQuanticMember().get(y);
              ans.getQuanticMember().merge(new BaseKey(j,y),coeJ.multiply(coeY), BigInteger::add);
          }
      }
      return ans;
  }

缺点

由于对应用设计模式的经验较为缺乏，架构设计时没有采用设计模式，存在显著的面向过程性
lexer和parser的实现时，复杂度过高。在hw1中把减号的语义去除，即parser的语义分割符仅为'+''*'，'-'仅作为Expr、Term、Single和Trigon的符号位，在后续作业的系数的符号=f(符号，指数)的转化时出了很多错误，例如负号外提出错sin(-1)**2化简成-sin(1)**2与识别负号位时未考虑pos==length的情况出错。同时parser的三个方法均出现了表示符号的参数的嵌套传递情况，debug时出现非常大的麻烦。

二、bug分析

第二次公测

自定义函数的函数声明中未考虑空格和tab，WA了两个点
第二次互测
lexer的一个分支忘记添加pos==length时return的终止条件，导致+-+1出现exception
反思：迭代开发作业可以使用之前作业的强测数据来测试本次作业的修改是否影响到之前的功能；做测试时不要忘记测试原先的基础功能是否维持正常
sin(-1)**2化简成-sin(1)**2,未考虑偶数次幂时消去负号的情况。~~反思：可能是初中的知识没学好~~
没有注意到互测的指数输入可以大于8
反思：公测时也要注意互测的数据规范；修改指数的数据范围时有一处遗漏导致出错
第一次和第三次作业未出现Bug
整体分析
总体来说，由于存储类的代码行和圈复杂度明显低于工作类，未出现计算方面的Bug。
Bug主要集中在lexer和parser的识别和解析字符串部分，此部分的圈复杂度较高，出现遗漏分支与修改不完善的情况。
输出部分的圈复杂度最高，针对此部分做的测试较多，未出现bug。

三、hack策略

自动化评测机测试时，对于数据生成程序的要求较高，当数据输入的限制较多与程序功能较为简单时，自动生成数据的强度不容易控制，容易出现数据较弱或不合法的情况。
根据被测程序构造样例的思路：
- 圈复杂度较高的环节：读入、输出、三角优化；
- 数据范围是否覆盖全面：例如sum的BigInteger
- 新增功能是否考虑全面：例如函数声明的空格和i**n的情况

四、心得体会

不要出现50行+的方法，否则Bug修复的时候有方法超过60行的风险Orz
为debug模式重写toString()便于调试，尤其是包含嵌套hashmap的类；满足作业化简要求的的输出单独建立print()方法
尽量在作业的开始阶段留出一定的可扩展空间，降低后续的修改规模&重构风险：比如作业1的时候偷懒按照幂次为单个char写的程序，不仅导致忘记幂次的前导符号和前导0，还导致作业2把幂次修改成大于8时只修改了lexer部分，后缀表达式有关幂次计算的部分忘记修改了；作业2的时候没有把sum和自定义函数作为字符串替换，而是在递归下降的过程中作为表达式因子替换，给作业3的嵌套函数留出了扩展性,作业3的相关功能也在作业2得到了测试;程序扩展一些额外的功能也意味着有更大的测试空间，对于数据生成程序的格式要求会降低，比如在作业1中不对括号层数和指数作限制时，测试的强度更高，数据生成程序也更简洁一些。

Next Post

BUAA-OS-Lab2
Previous Post

BUAA-C++与C#-项目分析报告

CATALOG